系统方块图,系统方块图概述

系统方块图概述

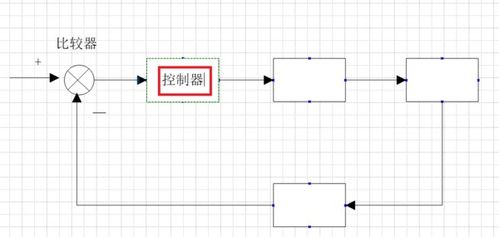
系统方块图是一种图形化的表示方法，用于描述系统的结构、功能以及信号流向。它广泛应用于工程、科学和数学等领域，特别是在自动控制系统中，方块图是一种重要的工具，可以帮助工程师和研究人员直观地理解和分析系统的动态行为。

系统方块图的基本元素

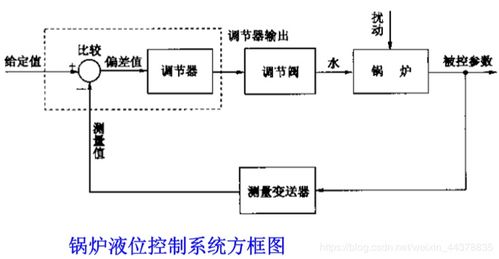
系统方块图由以下基本元素构成：

信号线：带有箭头的直线，箭头表示信号的传递方向，直线旁标记变量，即信号的时间函数或象函数。

信号引出点（线）：表示信号引出或测量的位置和传递方向。同一信号线上引出的信号，其性质、大小完全一样。

函数方块（环节）：传递函数的图解表示。函数方块具有运算功能，即对输入信号进行某种数学运算。

求和点（比较点、综合点）：信号之间代数加减运算的图解，用一个圆圈里面加上一个X及相应的信号箭头进行表示。每个箭头前方的“+”或“-”表示加上此信号或减去此信号。

系统方块图的建立步骤

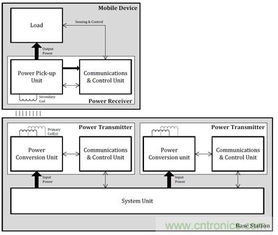
建立系统方块图通常遵循以下步骤：

建立系统各环节的微分方程，明确信号因果关系（输入/输出）。

对上述微分方程进行拉氏变换，绘制各环节的方框图。

按照信号在系统中的传递、变换过程，依次将各环节的方框图连接起来，得到系统的方块图。

系统方块图的应用

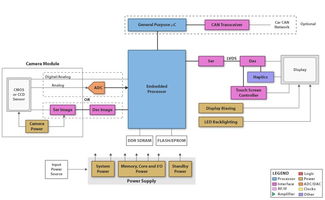
系统方块图在工程和科学领域有着广泛的应用，以下是一些常见的应用场景：

控制系统设计：通过方块图可以直观地分析系统的动态特性，为控制器的设计提供依据。

系统分析：方块图可以帮助工程师和研究人员理解系统的结构和功能，从而更好地进行系统分析和优化。

系统仿真：利用方块图可以建立系统的数学模型，并通过仿真软件进行系统性能的评估。

教学与培训：方块图是一种直观的教学工具，可以帮助学生和工程师更好地理解系统的工作原理。

系统方块图的优点

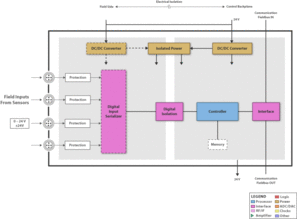
系统方块图具有以下优点：

直观性：方块图以图形化的方式展示系统结构，易于理解和分析。

灵活性：方块图可以根据需要添加或删除环节，方便进行系统设计和优化。

通用性：方块图适用于各种类型的系统，包括线性、非线性、连续和离散系统。

系统方块图的局限性

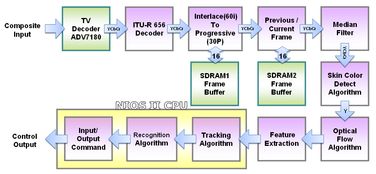
尽管系统方块图具有许多优点，但也存在一些局限性：

复杂性：对于复杂的系统，方块图可能过于复杂，难以理解和分析。

细节缺失：方块图主要展示系统的结构和功能，可能无法详细描述系统的实现细节。

动态特性：方块图主要关注系统的静态特性，对于系统的动态特性描述有限。

系统方块图是一种重要的图形化表示方法，在工程和科学领域有着广泛的应用。通过系统方块图，我们可以直观地理解系统的结构和功能，为系统设计、分析和优化提供有力支持。在实际应用中，我们也应注意到系统方块图的局限性，并结合其他工具和方法进行综合分析和评估。