信号与线性系统分析 pdf

引言

信号的基本概念

信号是信息传递的载体，它可以分为连续信号和离散信号。连续信号是指时间上连续变化的信号，如正弦波、方波等；离散信号是指时间上离散变化的信号，如数字信号等。信号分析主要包括时域分析、频域分析和复频域分析。

线性系统

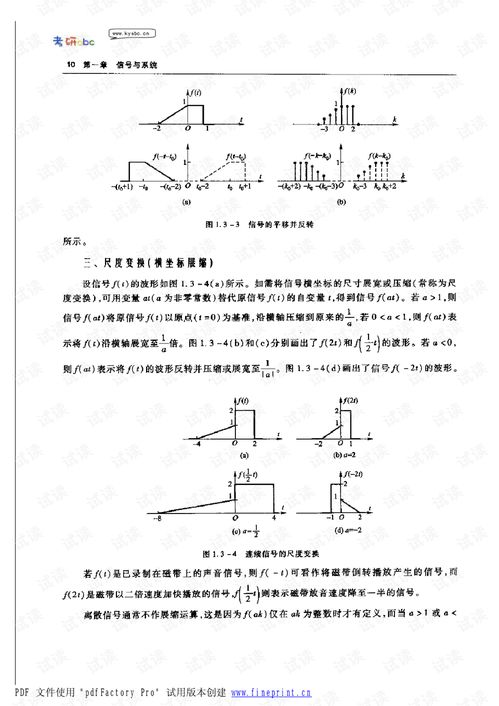
线性系统是指满足叠加原理和齐次性原理的系统。叠加原理是指多个信号同时作用于线性系统时，系统的输出等于各个信号单独作用于系统时的输出之和；齐次性原理是指当输入信号乘以一个常数时，输出信号也乘以相同的常数。线性系统在信号处理中具有重要作用，因为许多实际系统都可以近似为线性系统。

时域分析

时域分析是信号与线性系统分析的基础，它主要研究信号和系统在时间域内的特性。时域分析方法包括：时域波形分析、时域频谱分析、时域卷积等。时域分析可以帮助我们直观地了解信号和系统的动态特性。

频域分析

频域分析是信号与线性系统分析的重要方法，它将信号和系统从时域转换到频域进行分析。频域分析方法包括：傅里叶变换、拉普拉斯变换、Z变换等。频域分析可以帮助我们了解信号和系统的频率特性，以及系统对信号的滤波作用。

傅里叶变换

傅里叶变换是信号与线性系统分析中最重要的工具之一，它可以将信号从时域转换到频域。傅里叶变换具有以下特点：

线性：傅里叶变换满足叠加原理和齐次性原理。

唯一性：一个信号在时域和频域之间具有一一对应的关系。

可逆性：傅里叶变换是可逆的，即可以由频域信号恢复时域信号。

拉普拉斯变换

拉普拉斯变换是傅里叶变换在复频域的推广，它将信号从时域转换到复频域。拉普拉斯变换具有以下特点：

线性：拉普拉斯变换满足叠加原理和齐次性原理。

唯一性：一个信号在时域和复频域之间具有一一对应的关系。

可逆性：拉普拉斯变换是可逆的，即可以由复频域信号恢复时域信号。

系统函数

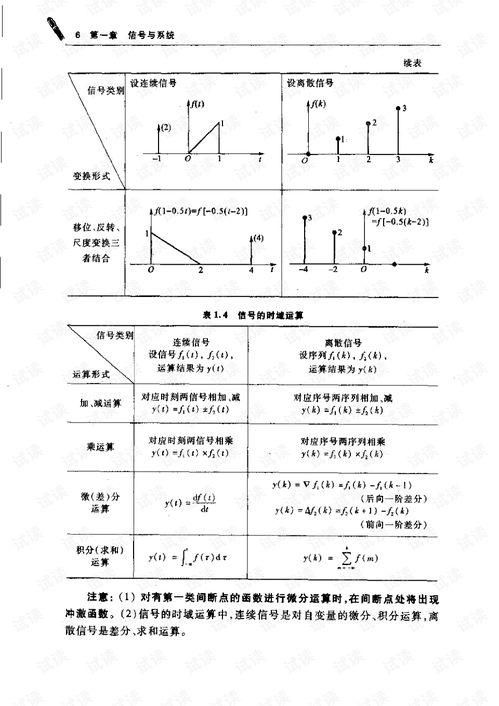
系统函数是描述线性系统特性的数学模型，它反映了系统对信号的滤波作用。系统函数可以是时域函数，也可以是频域函数。系统函数的求解方法包括：时域卷积、频域卷积、拉普拉斯变换等。

信号与线性系统分析的应用

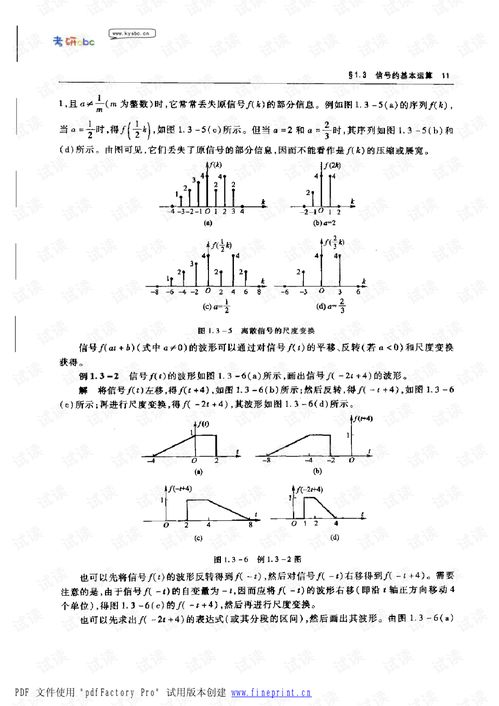
信号与线性系统分析在各个领域都有广泛的应用，以下列举几个典型应用：

通信系统：信号与线性系统分析在通信系统中用于信号调制、解调、滤波等。

信号处理：信号与线性系统分析在信号处理中用于信号去噪、压缩、增强等。

控制系统：信号与线性系统分析在控制系统中用于系统建模、控制器设计等。

图像处理：信号与线性系统分析在图像处理中用于图像滤波、压缩、增强等。

结论

信号与线性系统分析是电子工程、通信工程等领域的基础课程，它对于理解信号和系统的特性具有重要意义。本文介绍了信号与线性系统分析的基本概念、分析方法以及在实际应用中的重要性，希望对读者有所帮助。