信号与线性系统分析第六章答案,信号与线性系统分析第六章答案解析

信号与线性系统分析第六章答案解析

信号与线性系统分析是电子工程、通信工程等领域的重要基础课程。本章主要介绍了离散系统的频域分析，包括Z变换、系统函数、频率响应等内容。以下是对本章内容的详细解析及答案。

1. Z变换的定义及性质

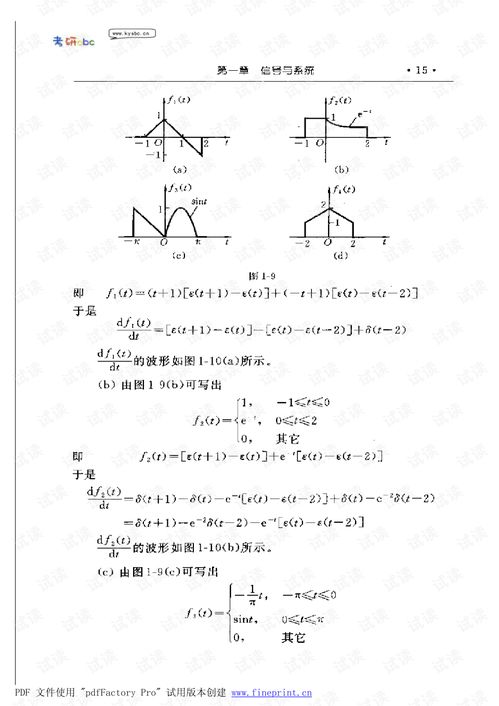
Z变换是离散时间信号的一种重要变换方法，它将离散时间信号转换为复频域上的函数。Z变换的定义如下：

设离散时间信号x[n]的Z变换为X(z)，则有：

X(z) = Σ[x[n]z^{-n}]，其中n为整数。

Z变换具有以下性质：

线性性质：若x[n]和y[n]的Z变换分别为X(z)和Y(z)，则ax[n] + by[n]的Z变换为aX(z) + bY(z)，其中a和b为常数。

移位性质：若x[n]的Z变换为X(z)，则x[n-n0]的Z变换为z^{-n0}X(z)，其中n0为任意整数。

尺度变换性质：若x[n]的Z变换为X(z)，则x[n] n的Z变换为zX'(z)，其中X'(z)为X(z)的导数。

初值定理：若x[n]的Z变换为X(z)，则x[0] = lim(z→1)X(z)。

终值定理：若x[n]的Z变换为X(z)，且X(z)在单位圆上的收敛半径大于1，则x[∞] = lim(z→0)zX(z)。

2. 系统函数的求解

系统函数H(z)是系统输入信号X(z)与输出信号Y(z)之间的关系，其定义为：

H(z) = Y(z) / X(z)

系统函数的求解方法有以下几种：

直接法：根据系统差分方程直接求解系统函数。

逆Z变换法：利用Z变换的性质和逆变换公式求解系统函数。

部分分式法：将系统函数分解为部分分式，然后求解各分式的逆Z变换。

3. 频率响应的求解

频率响应是系统函数在单位圆上的值，它描述了系统对不同频率信号的响应特性。频率响应的求解方法如下：

直接法：将系统函数H(z)在单位圆上展开为幂级数，然后取其实部得到频率响应。

逆Z变换法：利用Z变换的性质和逆变换公式求解频率响应。

部分分式法：将系统函数H(z)分解为部分分式，然后求解各分式的逆Z变换，最后取实部得到频率响应。

4. 系统稳定性分析

系统稳定性是系统性能的重要指标之一。根据系统函数H(z)的极点位置，可以判断系统的稳定性。以下为系统稳定性分析的方法：

极点位置法：若系统函数H(z)的所有极点均位于单位圆内，则系统稳定；若至少有一个极点位于单位圆外，则系统不稳定。

收敛域法：若系统函数H(z)的收敛域包含单位圆，则系统稳定；若收敛域不包含单位圆，则系统不稳定。

本章介绍了离散系统的频域分析，包括Z变换、系统函数、频率响应等内容。通过学习本章内容，读者可以掌握离散系统频域分析的基本方法，为后续学习信号处理、通信系统等课程打下基础。

以上是对信号与线性系统分析第六章答案的解析，希望对读者有所帮助。