lti系统的冲激响应,什么是LTI系统

线性时不变（LTI）系统是信号与系统领域中一个重要的概念。在工程实践中，许多系统都可以近似为LTI系统。本文将详细介绍LTI系统的冲激响应，包括其定义、性质、求解方法以及在实际应用中的重要性。

什么是LTI系统

线性时不变（LTI）系统是指系统满足线性性和时不变性两个条件的系统。线性性意味着系统对于任意两个输入信号的叠加和任意一个输入信号的缩放，其输出信号也是这两个输入信号输出信号的叠加和缩放。时不变性意味着系统的特性不随时间变化，即系统在任意时刻的响应与在任意时刻的输入信号进行卷积的结果相同。

冲激响应的定义

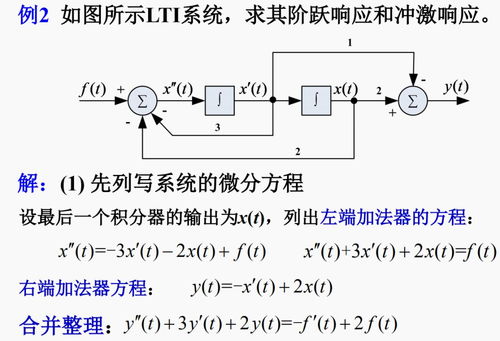
冲激响应是LTI系统的一个重要概念，它描述了系统对于单位冲激信号的响应。单位冲激信号是一个在时间轴上只有一个无穷小值（即冲激）的信号，其数学表达式为δ(t)。当单位冲激信号作用于LTI系统时，系统的输出称为冲激响应，记为h(t)。

冲激响应的性质

冲激响应具有以下性质：

线性性：冲激响应满足线性性质，即对于任意两个输入信号f(t)和g(t)，以及任意常数a和b，有h(at + bg(t)) = ah(t) + bh(g(t))。

时不变性：冲激响应满足时不变性质，即对于任意时间t0，有h(t - t0) = h(t) δ(t - t0)。

因果性：冲激响应满足因果性，即系统的输出只能由当前和过去的输入信号决定，与未来的输入信号无关。

冲激响应的求解方法

求解LTI系统的冲激响应主要有以下几种方法：

时域卷积法：根据卷积定理，LTI系统的冲激响应可以通过输入信号与系统函数的卷积积分得到。具体公式为：h(t) = (f(t) h(t))，其中f(t)为输入信号，h(t)为系统函数。

频域分析法：利用傅里叶变换，可以将时域卷积转化为频域乘积。具体公式为：H(jω) = F(jω) H(jω)，其中F(jω)为输入信号的傅里叶变换，H(jω)为系统函数的傅里叶变换。

微分方程法：对于线性微分方程描述的LTI系统，可以通过求解微分方程得到冲激响应。

冲激响应在实际应用中的重要性

冲激响应在信号与系统领域具有重要的实际应用价值，主要体现在以下几个方面：

系统分析：通过分析冲激响应，可以了解系统的稳定性和频率响应特性。

系统设计：在设计LTI系统时，可以根据冲激响应来优化系统的性能。

信号处理：在信号处理领域，冲激响应可以用于信号滤波、信号检测等应用。

结论

本文介绍了LTI系统的冲激响应，包括其定义、性质、求解方法以及在实际应用中的重要性。通过学习冲激响应，有助于我们更好地理解和应用LTI系统，为工程实践提供理论支持。