lti系统的系统函数,系统函数的定义

线性时不变（Linear Time-Invariant，LTI）系统是信号处理和系统理论中的基本概念。在通信、控制、图像处理等领域，LTI系统扮演着至关重要的角色。本文将详细介绍LTI系统的系统函数，包括其定义、性质、应用以及求解方法。

系统函数的定义

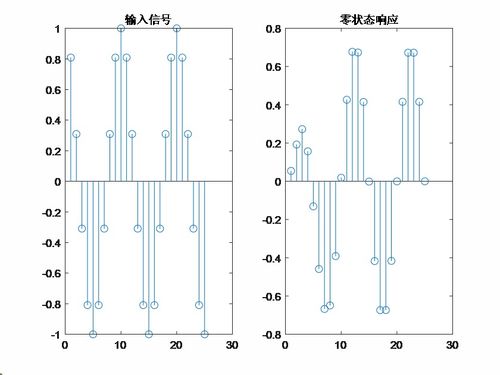
系统函数是描述LTI系统输入与输出之间关系的数学工具。对于一个离散时间LTI系统，其系统函数H(z)定义为输入信号的Z变换与输出信号的Z变换之比，即：

[ H(z) = frac{Y(z)}{X(z)} ]

其中，X(z)和Y(z)分别表示输入信号和输出信号的Z变换。

系统函数的性质

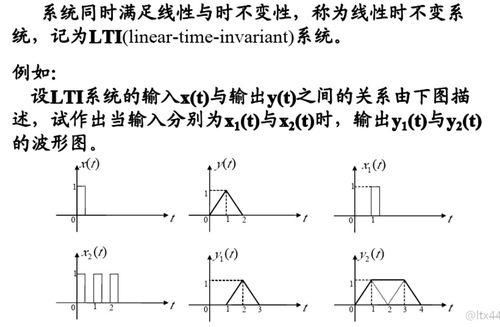
系统函数具有以下性质：

线性性：系统函数满足叠加原理，即对于任意两个输入信号x1(n)和x2(n)，以及相应的输出信号y1(n)和y2(n)，有：

( H(z) left[ x_1(n) + x_2(n) right] = H(z) x_1(n) + H(z) x_2(n) )

时不变性：系统函数不随时间变化，即对于任意时间延迟的输入信号x(n-k)，其输出信号为y(n-k)，系统函数保持不变。

( H(z) x(n-k) = x(n-k) H(z) )

因果性：系统函数的输出只依赖于当前和过去的输入，不依赖于未来的输入。

( H(z) x(n) = x(n) H(z) )

系统函数的应用

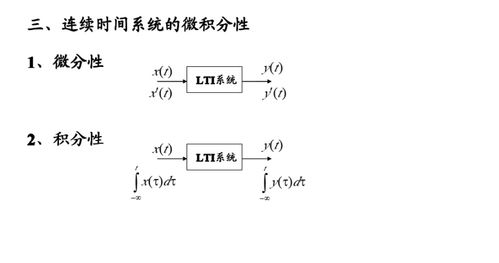
系统函数在信号处理和系统理论中具有广泛的应用，以下列举几个例子：

滤波器设计：通过设计合适的系统函数，可以实现低通、高通、带通、带阻等滤波器。

系统分析：利用系统函数可以分析系统的稳定性、频率响应等特性。

信号处理：系统函数可以用于信号压缩、信号恢复等处理过程。

系统函数的求解方法

求解系统函数的方法主要有以下几种：

差分方程法：根据系统的差分方程，通过求解Z变换得到系统函数。

单位冲激响应法：根据系统的单位冲激响应，通过求解卷积得到系统函数。

频率响应法：根据系统的频率响应，通过求解傅里叶变换得到系统函数。

结论

系统函数是描述LTI系统输入与输出之间关系的数学工具，具有线性、时不变、因果等性质。在信号处理和系统理论中，系统函数具有广泛的应用。本文介绍了系统函数的定义、性质、应用以及求解方法，为读者提供了关于LTI系统函数的全面了解。

参考文献

1. Oppenheim, A. V., Willsky, A. S., & Hamid, I. (2015). Signals and systems. Pearson.

2. Proakis, J. G., & Manolakis, D. G. (1996). Digital signal processing: principles, algorithms, and applications. Prentice Hall.

3. Oppenheim, A. V., & Schafer, R. W. (1975). Discrete-time signal processing. Prentice Hall.