fir系统函数,数字信号处理中的关键概念

FIR系统函数：数字信号处理中的关键概念

在数字信号处理（DSP）领域，FIR（有限脉冲响应）滤波器因其线性相位特性和易于实现的优点而备受关注。本文将深入探讨FIR系统函数的概念、特性及其在数字信号处理中的应用。

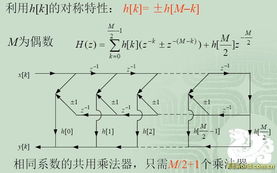
FIR系统函数是描述有限脉冲响应滤波器性能的核心数学工具。它通过一个差分方程来定义，该方程描述了滤波器输出与输入信号之间的关系。具体来说，一个N阶FIR滤波器的系统函数可以表示为：

H(z) = Σ[bk z-k]

其中，H(z)是系统函数，bk是滤波器的系数，z是复变量，k是时间索引。

系统函数H(z)的物理意义在于它描述了滤波器对输入信号的响应。通过分析H(z)，我们可以了解滤波器的频率响应、稳定性以及线性相位特性。例如，当z=1时，H(z)的值等于滤波器的单位脉冲响应，即滤波器对单位脉冲信号的响应。

FIR滤波器具有以下特点：

线性相位：FIR滤波器具有线性相位特性，这意味着滤波器不会改变信号的相位，这对于保持信号波形至关重要。

稳定性：FIR滤波器总是稳定的，因为其系统函数的极点全部位于单位圆内。

易于实现：FIR滤波器可以通过简单的乘法和加法运算实现，这使得它在硬件和软件实现中都非常方便。

FIR滤波器的设计方法主要包括窗函数法、频率抽样法和最小二乘法等。以下简要介绍这三种方法：

窗函数法：通过选择合适的窗函数，将理想滤波器的频率响应截断，从而得到FIR滤波器的频率响应。

频率抽样法：通过在单位圆上等间隔地取点，得到理想滤波器的频率响应，然后通过插值得到FIR滤波器的频率响应。

最小二乘法：通过最小化误差函数，找到一组系数，使得FIR滤波器的频率响应与理想滤波器的频率响应尽可能接近。

FIR滤波器在数字信号处理领域有着广泛的应用，以下列举一些典型应用：

信号滤波：去除信号中的噪声和干扰，提高信号质量。

信号变换：将信号从一种形式转换为另一种形式，如时域到频域的转换。

信号压缩：减少信号的存储空间和传输带宽。

图像处理：去除图像中的噪声和干扰，提高图像质量。

本文介绍了FIR系统函数的概念、特性、设计方法及其应用。FIR滤波器因其线性相位、稳定性和易于实现等优点，在数字信号处理领域得到了广泛应用。随着数字信号处理技术的不断发展，FIR滤波器将在更多领域发挥重要作用。