logistic 混沌系统,Logistic混沌系统的原理与应用

Logistic混沌系统的原理与应用

Logistic混沌系统是一种典型的非线性动力学系统，它起源于对人口增长模型的研究。Logistic映射是最简单的离散混沌系统之一，其表达式为：( x_{n+1} = r cdot x_n cdot (1 - x_n) )，其中，( x_n )为第n次迭代的系统状态，( r )为控制参数。本文将介绍Logistic混沌系统的原理、特性及其在各个领域的应用。

Logistic混沌系统的特性

Logistic混沌系统具有以下特性：

对初始条件敏感：混沌系统对初始条件的微小变化非常敏感，这意味着即使初始条件只相差一个很小的量，系统的演化轨迹也会产生巨大的差异。

非周期性：混沌系统的演化轨迹是非周期的，即没有固定的周期性模式。

混沌吸引子：混沌系统在演化过程中会逐渐收敛到一个稳定的吸引子，吸引子可以是点、线、面或更复杂的结构。

混沌窗口：在Logistic映射中，当控制参数( r )在某个特定区间内时，系统会表现出混沌行为，这个区间被称为混沌窗口。

Logistic混沌系统的应用

密码学：混沌系统可以产生具有伪随机性的序列，用于加密通信，提高通信安全性。

图像加密：利用混沌系统的特性，可以对图像进行加密和解密，保护图像信息不被非法获取。

语音加密：混沌系统可以用于语音信号的加密和解密，确保语音通信的安全性。

生物信息学：混沌理论在生物信息学领域也有应用，如研究生物种群的增长、细胞分裂等。

经济学：混沌理论可以用于分析经济系统的动态行为，预测经济波动。

Logistic混沌系统的优化与改进

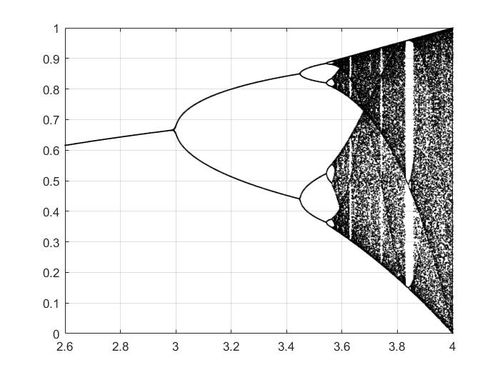
控制参数优化：通过调整控制参数( r )的值，可以改变混沌系统的行为，提高系统的复杂性和安全性。

混沌映射改进：设计新的混沌映射，提高混沌序列的复杂性和随机性。

混沌系统融合：将Logistic混沌系统与其他混沌系统或加密算法相结合，提高系统的整体性能。

Logistic混沌系统作为一种典型的非线性动力学系统，具有对初始条件敏感、非周期性、混沌吸引子等特性。它在密码学、图像加密、语音加密、生物信息学、经济学等领域都有广泛的应用。随着研究的深入，Logistic混沌系统将会在更多领域发挥重要作用。