matlab信号与系统实例,连续信号采样与恢复

MATLAB信号与系统实例分析：连续信号采样与恢复

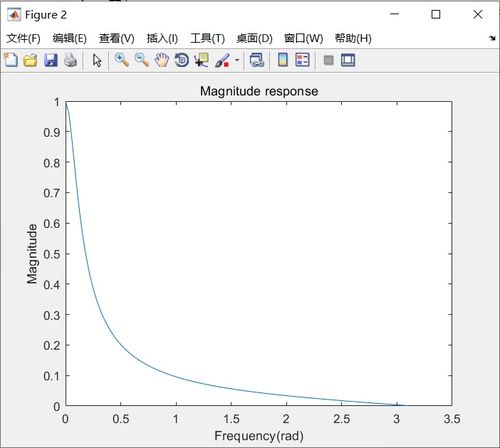
在信号与系统中，连续信号的采样与恢复是一个重要的研究课题。本文将利用MATLAB软件，通过一个具体的实例来分析连续信号的采样与恢复过程，帮助读者更好地理解这一概念。

信号与系统是电子工程、通信工程等领域的基础课程。在信号处理过程中，连续信号的采样与恢复是至关重要的环节。通过对连续信号进行采样，可以将连续信号转换为离散信号，便于后续处理。而恢复过程则是将离散信号还原为连续信号，以实现信号的传输、存储和再现。本文将利用MATLAB软件，通过一个具体的实例来分析连续信号的采样与恢复过程。

二、实例介绍

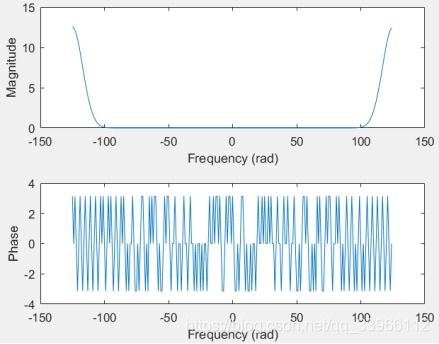
本文以一个简单的连续信号——正弦信号为例，分析其采样与恢复过程。正弦信号的表达式为：f(t) = A sin(ωt + φ)，其中A为振幅，ω为角频率，φ为初相位。为了便于分析，我们选取A=1，ω=2π，φ=0。

三、采样过程

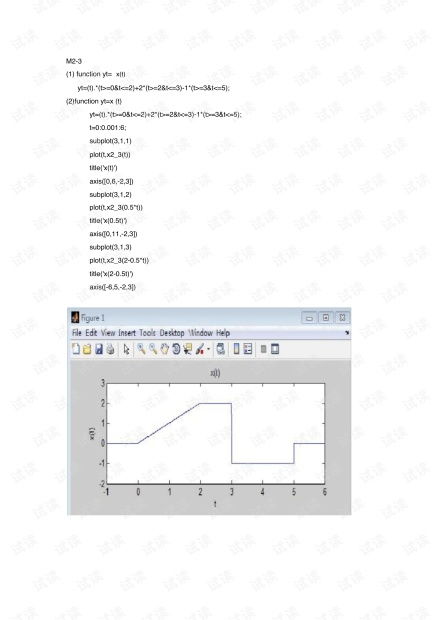
在MATLAB中，我们可以使用内置函数`sample`来实现连续信号的采样。首先，我们需要定义采样周期T和采样点数N。在本例中，我们选取采样周期T=0.1，采样点数N=100。接下来，使用`sample`函数对连续信号进行采样，得到离散信号。

```matlab

% 定义采样周期和采样点数

T = 0.1;

N = 100;

% 定义连续信号参数

A = 1;

omega = 2pi;

phi = 0;

% 定义时间向量

t = 0:T:(N-1)T;

% 定义连续信号

f = A sin(omega t + phi);

% 采样连续信号

fs = sample(f, T);

四、恢复过程

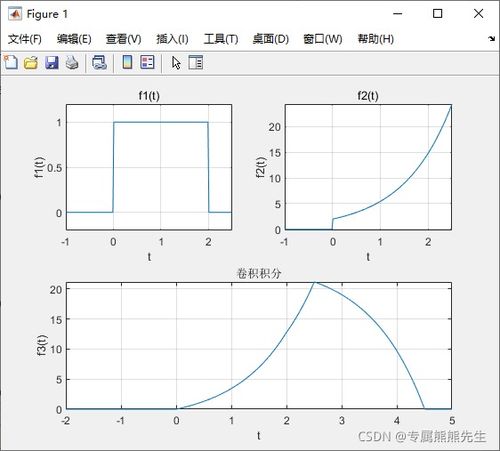
在MATLAB中，我们可以使用内置函数`recover`来实现离散信号的恢复。首先，我们需要定义恢复信号的采样周期T'和采样点数N'。在本例中，我们选取恢复信号的采样周期T'=0.01，采样点数N'=1000。接下来，使用`recover`函数对离散信号进行恢复，得到连续信号。

```matlab

% 定义恢复信号的采样周期和采样点数

T_prime = 0.01;

N_prime = 1000;

% 恢复离散信号

f_recovered = recover(fs, T_prime);

五、结果分析

通过上述代码，我们得到了连续信号f(t)的采样信号fs和恢复信号f_recovered。为了分析采样与恢复过程的效果，我们可以绘制原始信号、采样信号和恢复信号的波形图，并计算恢复信号的均方误差（MSE）。

```matlab

% 绘制原始信号、采样信号和恢复信号的波形图

figure;

subplot(3,1,1);

plot(t, f);

title('原始信号');

xlabel('时间t');

ylabel('幅度');

subplot(3,1,2);

plot(t, fs);

title('采样信号');

xlabel('时间t');

ylabel('幅度');

subplot(3,1,3);

plot(t, f_recovered);

title('恢复信号');

xlabel('时间t');

ylabel('幅度');

% 计算恢复信号的均方误差

mse = mean((f_recovered - f).^2);

fprintf('恢复信号的均方误差为：%f

', mse);

六、结论

本文通过MATLAB软件，对连续信号的采样与恢复过程进行了实例分析。结果表明，在合适的采样周期和恢复信号参数下，我们可以有效地对连续信号进行采样和恢复。这为信号处理领域的研究和应用提供了有益的参考。