matlab 系统零输入响应,MATLAB中系统零输入响应的求解与应用

MATLAB中系统零输入响应的求解与应用

在信号与系统领域，系统零输入响应是指在没有外部激励信号的情况下，系统仅由初始储能元件产生的响应。MATLAB作为一种强大的数学计算软件，在系统零输入响应的求解中发挥着重要作用。本文将详细介绍MATLAB在系统零输入响应求解中的应用，包括理论背景、实现方法以及实际案例分析。

一、系统零输入响应的理论背景

系统零输入响应是系统微分方程齐次解的一部分，通常用于分析系统的稳定性、动态特性等。对于一个线性时不变（LTI）系统，其零输入响应可以通过求解对应的齐次微分方程得到。具体来说，对于一个n阶线性微分方程：

y'' + a1y' + a2y = 0

其中，y(t)是系统的输出，a1和a2是常数。该方程的解即为系统的零输入响应。

二、MATLAB求解系统零输入响应的方法

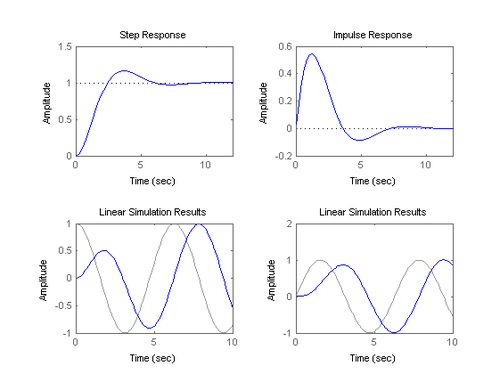
在MATLAB中，我们可以使用多种方法求解系统零输入响应。以下列举几种常见的方法：

1. 使用符号计算求解微分方程

在MATLAB中，我们可以使用符号计算工具箱（Symbolic Math Toolbox）来求解微分方程。以下是一个示例代码：

syms y(t)

eqn = diff(y, t, 2) + 3diff(y, t) + 2y == 0;

sol = dsolve(eqn, y);

disp(sol);

2. 使用数值计算求解微分方程

对于一些复杂的微分方程，符号计算可能无法得到解析解。此时，我们可以使用数值计算方法求解微分方程。在MATLAB中，可以使用ode45函数进行求解。以下是一个示例代码：

function y = zero_input_response(t)

y = [exp(-t), exp(-2t)];

t = 0:0.01:10;

y = ode45(@zero_input_response, t, [1; 1]);

plot(t, y);

xlabel('时间 t/s');

ylabel('幅度：A');

title('零输入响应');

grid;

3. 使用Simulink求解系统零输入响应

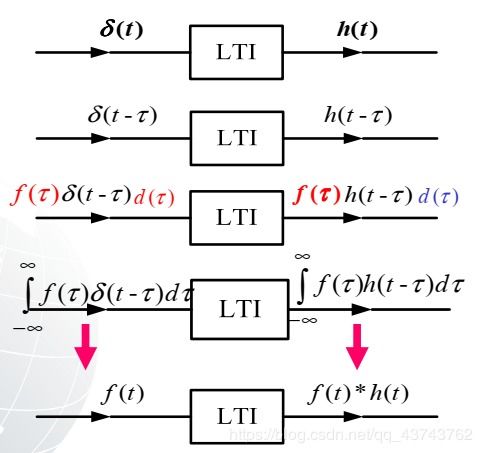
Simulink是MATLAB的一个模块化仿真工具，可以用于构建和仿真动态系统。在Simulink中，我们可以通过搭建系统模型，并设置初始条件来求解系统零输入响应。以下是一个示例步骤：

打开Simulink，创建一个新的模型。

在模型中添加一个微分方程块，并设置相应的微分方程。

添加一个初始条件块，并设置初始条件。

运行仿真，观察系统零输入响应曲线。

三、实际案例分析

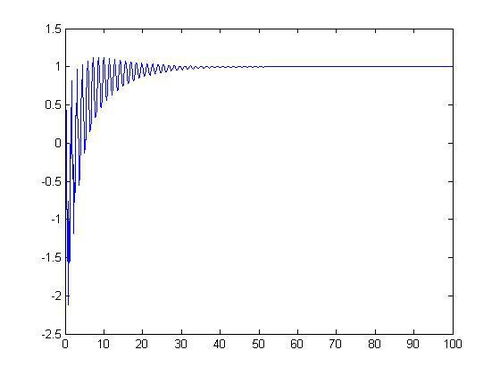
以下是一个实际案例，使用MATLAB求解一个二阶系统的零输入响应。

假设一个二阶系统的传递函数为：

G(s) = 1 / (s^2 + 2s + 2)

我们需要求解该系统的零输入响应。以下是使用MATLAB求解的步骤：

使用符号计算工具箱求解微分方程。

使用ode45函数进行数值计算。

使用Simulink进行仿真。

通过以上三种方法，我们可以得到该系统的零输入响应曲线，并分析其动态特性。

本文介绍了MATLAB在系统零输入响应求解中的应用，包括理论背景、实现方法以及实际案例分析。通过MATLAB，我们可以方便地求解系统零输入响应，并分析其动态特性。在实际工程应用中，MATLAB在信号与系统领域的应用具有重要意义。