matlab 线性时不变系统,线性时不变系统的定义

线性时不变系统（Linear Time-Invariant, LTI）是数字信号处理和系统理论中的基本概念。在MATLAB中，对线性时不变系统的分析和设计是至关重要的。本文将介绍如何在MATLAB中创建、分析和仿真线性时不变系统，并探讨其相关性质和应用。

线性时不变系统的定义

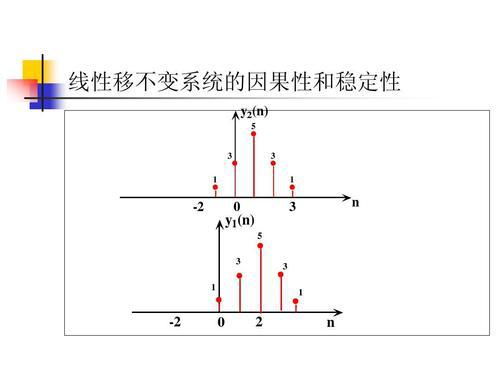
线性时不变系统是指系统对于输入信号的响应满足线性性和时不变性。线性性意味着系统的输出是输入的线性组合，而时不变性则表示系统的响应不随时间变化。具体来说，如果输入信号为( x[n] )，输出信号为( y[n] )，则系统满足以下条件：

线性性：( y[n] = c_1x_1[n] + c_2x_2[n] )，其中( c_1 )和( c_2 )为常数。

时不变性：如果输入信号( x[n] )变为( x[n-n_0] )，则输出信号( y[n] )也变为( y[n-n_0] )。

在MATLAB中创建线性时不变系统

filter：用于计算离散时间系统的输出。

tf：用于创建传递函数模型。

zplane：用于绘制系统的零点和极点。

以下是一个简单的例子，演示如何使用MATLAB创建一个线性时不变系统并计算其输出：

function [y] = linear_system(x)

% 定义系统系数

b = [1 -2 1];

a = [1 -1.5 0.5];

% 计算输出

y = filter(b, a, x);

分析线性时不变系统的性质

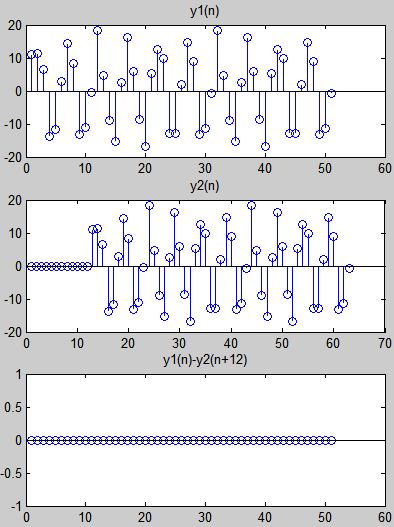
线性时不变系统具有以下重要性质：

叠加原理：如果系统对两个输入信号的响应分别为( y_1[n] )和( y_2[n] )，则系统对它们的线性组合( c_1y_1[n] + c_2y_2[n] )的响应为( c_1y_1[n] + c_2y_2[n] )。

时不变性：如果输入信号( x[n] )变为( x[n-n_0] )，则输出信号( y[n] )也变为( y[n-n_0] )。

因果性：系统的输出只依赖于当前和过去的输入，而不依赖于未来的输入。

稳定性：对于所有有界输入，系统输出也是有界的。

以下是一个使用MATLAB分析线性时不变系统稳定性的例子：

function [is_stable] = check_stability(a)

% 判断系统是否稳定

is_stable = all(abs(roots(a)) < 1);

仿真线性时不变系统

linspace：用于生成线性间隔的向量。

plot：用于绘制系统输出。

simulink：用于创建和仿真复杂系统。

以下是一个使用MATLAB仿真线性时不变系统的例子：

function simulate_linear_system()

% 定义输入信号

x = linspace(0, 1, 100);

% 创建系统

sys = tf([1 -2 1], [1 -1.5 0.5]);

% 计算输出

y = lsim(sys, x, 0:1);

% 绘制输出

plot(y);

xlabel('时间');

ylabel('输出');

结论

线性时不变系统在数字信号处理和系统理论中扮演着重要角色。在MATLAB中，我们可以方便地创建、分析和仿真线性时不变系统。通过本文的介绍，读者可以了解到如何在MATLAB