matlab 线性系统理论,线性系统建模

线性系统理论是自动控制、信号处理、通信系统等领域的基础理论之一。MATLAB作为一种功能强大的科学计算软件，在线性系统理论的学习和研究中发挥着重要作用。本文将介绍MATLAB在线性系统理论中的应用，包括系统建模、稳定性分析、能控性和能观性判断等。

线性系统建模

传递函数模型：使用`tf`函数创建传递函数模型，例如：`sys = tf([1 2], [1 3 2])`，其中分子系数为 `[1 2]`，分母系数为 `[1 3 2]`。

状态空间模型：使用`ss`函数创建状态空间模型，例如：`sys = ss([1 2; 3 4], [5 6], [7 8], [9 10])`，其中状态矩阵为 `[1 2; 3 4]`，输入矩阵为 `[5 6]`，输出矩阵为 `[7 8]`，直接传递矩阵为 `[9 10]`。

零极点模型：使用`zpk`函数创建零极点模型，例如：`sys = zpk([1 2], [3 4], [5 6])`，其中零点为 `[1 2]`，极点为 `[3 4]`，增益为 `[5 6]`。

稳定性分析

根轨迹分析：使用`rlocus`函数绘制根轨迹，例如：`rlocus(sys)`。

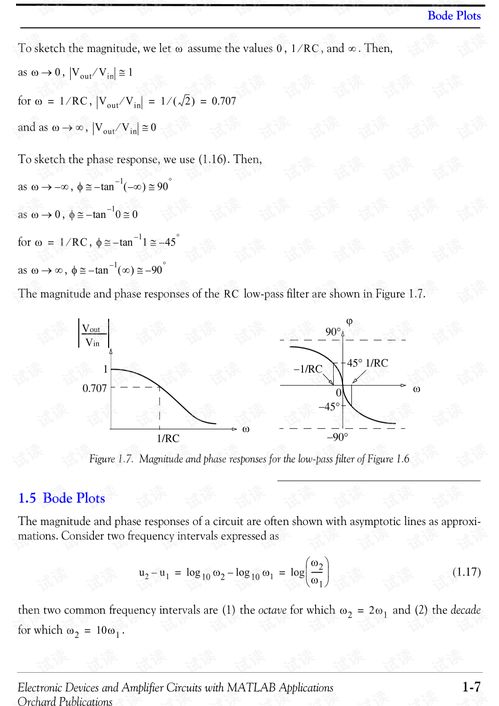
Bode图分析：使用`bode`函数绘制Bode图，例如：`bode(sys)`。

Nyquist图分析：使用`nyquist`函数绘制Nyquist图，例如：`nyquist(sys)`。

李雅普诺夫稳定性分析：使用`lyapunov`函数进行李雅普诺夫稳定性分析，例如：`[V, E] = lyapunov(sys)`，其中`V`为李雅普诺夫函数，`E`为特征值。

能控性和能观性判断

能控性和能观性是线性系统理论中的重要概念。在MATLAB中，可以使用以下方法判断线性系统的能控性和能观性：

能控性判断：使用`controllability`函数判断线性系统的能控性，例如：`[C, E] = controllability(sys)`，其中`C`为能控性矩阵，`E`为特征值。

能观性判断：使用`observability`函数判断线性系统的能观性，例如：`[O, E] = observability(sys)`，其中`O`为能观性矩阵，`E`为特征值。

状态反馈与闭环极点配置

状态反馈与闭环极点配置是线性系统理论中的重要内容。在MATLAB中，可以使用以下方法进行状态反馈与闭环极点配置：

状态反馈：使用`place`函数进行状态反馈，例如：`K = place(sys, [1 2 3])`，其中`K`为状态反馈矩阵，`[1 2 3]`为期望的闭环极点。

闭环极点配置：使用`poles`函数进行闭环极点配置，例如：`poles(sys)`，其中返回系统的闭环极点。

状态观测器

状态观测器是线性系统理论中的重要工具。在MATLAB中，可以使用以下方法设计状态观测器：

李雅普诺夫观测器：使用`lyapunov`函数设计李雅普诺夫观测器，例如：`[V, E] = lyapunov(sys)`。