matlab离散系统,深入探讨MATLAB在离散系统分析中的应用

深入探讨MATLAB在离散系统分析中的应用

随着计算机技术的飞速发展，MATLAB作为一种功能强大的科学计算软件，在各个领域得到了广泛应用。在离散系统分析领域，MATLAB凭借其丰富的工具箱和灵活的编程环境，成为了研究人员和工程师们不可或缺的工具。

一、离散系统的基本概念

离散系统是指系统的输入和输出信号在时间上不连续，且具有固定的时间间隔。与连续系统相比，离散系统在信号处理、控制理论等领域具有独特的优势。离散系统分析主要包括时域分析、频域分析和Z域分析等。

二、MATLAB在离散系统时域分析中的应用

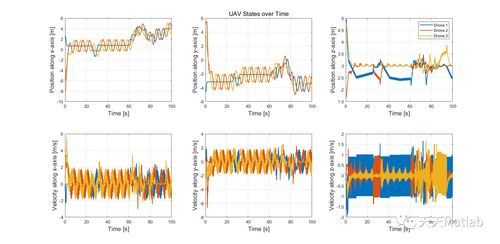
时域分析是离散系统分析的基础，主要研究系统在时域内的特性。在MATLAB中，我们可以利用以下工具进行时域分析：

filter()函数：用于求解离散系统差分方程的数值解。

conv()函数：用于计算离散时间序列的卷积。

linspace()函数：用于生成等间隔的离散时间序列。

以下是一个使用filter()函数求解离散系统差分方程的示例：

num = [1, -1.6, 1.28]; % 系统差分方程的分子系数

den = [1, -0.5, 0.1]; % 系统差分方程的分母系数

t = linspace(0, 10, 100); % 生成时间序列

x = [1, 0, 0]; % 输入序列

y = filter(num, den, x); % 求解系统响应

plot(t, y); % 绘制系统响应曲线

xlabel('时间');

ylabel('输出');

title('离散系统时域分析');

三、MATLAB在离散系统频域分析中的应用

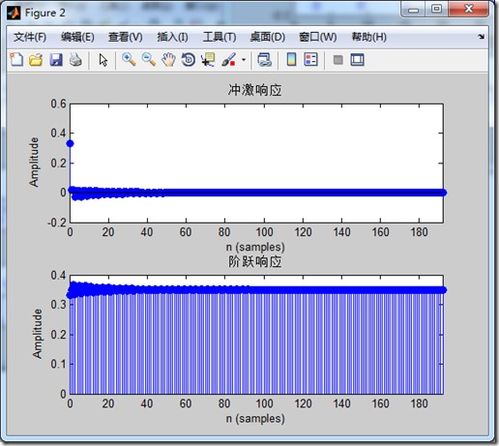
频域分析是离散系统分析的重要手段，主要研究系统在频域内的特性。在MATLAB中，我们可以利用以下工具进行频域分析：

fft()函数：用于计算离散时间序列的快速傅里叶变换（FFT）。

ifft()函数：用于计算离散时间序列的逆快速傅里叶变换（IFFT）。

freqz()函数：用于绘制离散系统的频率响应曲线。

以下是一个使用fft()函数计算离散时间序列的FFT的示例：

x = [1, 2, 3, 4, 5]; % 离散时间序列

X = fft(x); % 计算FFT

N = length(x); % 序列长度

f = linspace(0, 1, N); % 频率序列

plot(f, abs(X/N)); % 绘制FFT结果

xlabel('频率');

ylabel('幅度');

title('离散系统频域分析');

四、MATLAB在离散系统Z域分析中的应用

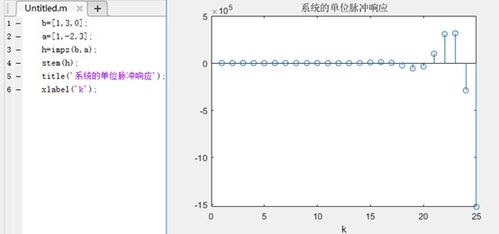
Z域分析是离散系统分析的重要方法，主要研究系统在Z域内的特性。在MATLAB中，我们可以利用以下工具进行Z域分析：

zplane()函数：用于绘制离散系统转移函数的零、极点分布图。

tf2zp()函数：用于将系统传递函数转换为零、极点形式。

以下是一个使用zplane()函数绘制离散系统转移函数零、极点分布图的示例：

num = [1, -1.6, 1.28]; % 系统差分方程的分子系数

den = [1, -0.5, 0.1]; % 系统差分方程的分母系数

zplane(num, den); % 绘制零、极点分布图

xlabel('z平面');

ylabel('z平面');

title('离散系统Z域分析');

MATLAB在离散系统分析中具有广泛的应用，可以帮助我们快速、准确地分析