matlab求系统的阶跃响应,准备环境

在自动控制领域，系统的阶跃响应是评估系统动态性能的重要手段。阶跃响应指的是系统在输入信号发生阶跃变化时的输出响应。通过分析阶跃响应，我们可以了解系统的稳定性、快速性和准确性。本文将介绍如何使用MATLAB求解系统的阶跃响应，并分析相关性能指标。

准备环境

在开始之前，请确保您的MATLAB环境中已安装控制系统工具箱（Control System Toolbox）。如果没有安装，请先进行安装。

创建系统模型

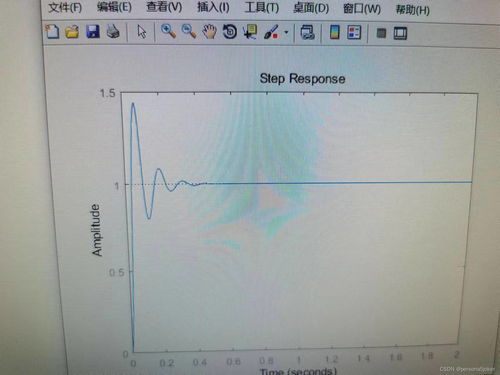
首先，我们需要创建一个系统模型。在MATLAB中，可以使用`tf`函数创建传递函数模型。以下是一个一阶系统的例子：

```matlab

s = tf('s');

sys = 1/(s + 1);

这里，`s`是拉普拉斯变换中的复变量，`tf`函数创建了一个传递函数模型，其中分子为1，分母为`s + 1`。这个系统是一个一阶系统，其时间常数`τ = 1`。

求解阶跃响应

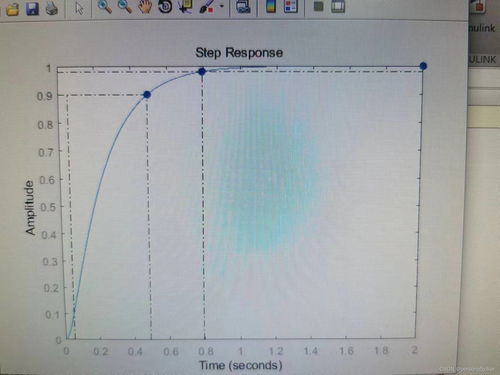
使用`step`函数可以求解系统的阶跃响应。以下是一个求解上述一阶系统阶跃响应的例子：

```matlab

t = 0:0.01:10; % 定义时间向量

y = step(sys, t); % 求解阶跃响应

plot(t, y); % 绘制阶跃响应曲线

title('一阶系统的阶跃响应'); % 添加标题

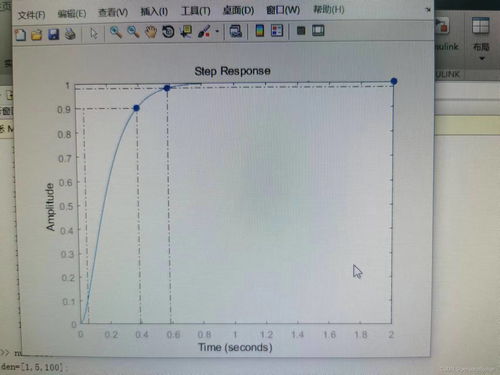
运行上述代码后，将得到一阶系统的阶跃响应曲线。从图中可以看出，系统在0.61秒时达到稳态值，上升时间为0.61秒，调整时间为0.61秒。

分析阶跃响应性能指标

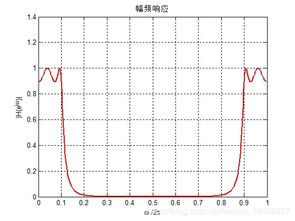
阶跃响应性能指标主要包括上升时间、调整时间、峰值时间、超调量和稳态误差。以下是如何计算这些指标的MATLAB代码：

```matlab

% 计算上升时间

rise_time = find(y >= 1 - 0.02, 1);

rise_time = rise_time(1) / t(1);

% 计算调整时间

settling_time = find(abs(y - 1) = max(y), 1);

peak_time = peak_time(1) / t(1);

% 计算超调量

overshoot = max(y) - 1;

% 计算稳态误差

steady_state_error = 1 - min(y);

% 输出性能指标

fprintf('上升时间: %.2f 秒

', rise_time);

fprintf('调整时间: %.2f 秒

', settling_time);

fprintf('峰值时间: %.2f 秒

', peak_time);

fprintf('超调量: %.2f%%

', overshoot 100);

fprintf('稳态误差: %.2f

', steady_state_error);

运行上述代码后，将输出一阶系统的阶跃响应性能指标。根据计算结果，我们可以评估系统的动态性能。

本文介绍了如何使用MATLAB求解系统的阶跃响应，并分析了相关性能指标。通过阶跃响应，我们可以了解系统的动态性能，为系统设计和优化提供依据。在实际应用中，可以根据需要调整时间向量`t`的步长，以获得更精确的阶跃响应曲线和性能指标。