matlab求系统极点,系统极点的基本概念

在自动控制领域，系统的极点对于分析系统的动态特性和稳定性至关重要。MATLAB作为一种强大的数学计算软件，提供了丰富的工具和函数来求解系统的极点。本文将详细介绍如何在MATLAB中求解系统的极点，包括基本概念、常用函数以及实际应用案例。

系统极点的基本概念

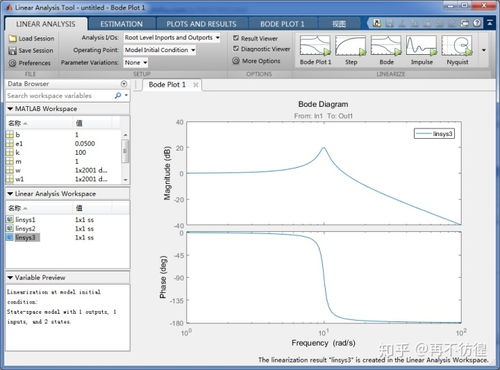
系统极点是指使系统传递函数分母为零的根。对于传递函数G(s) = N(s)/D(s)，其中N(s)是分子多项式，D(s)是分母多项式，极点就是D(s)的根。极点的位置决定了系统的稳定性、响应速度和超调量等动态特性。

MATLAB求解极点的常用函数

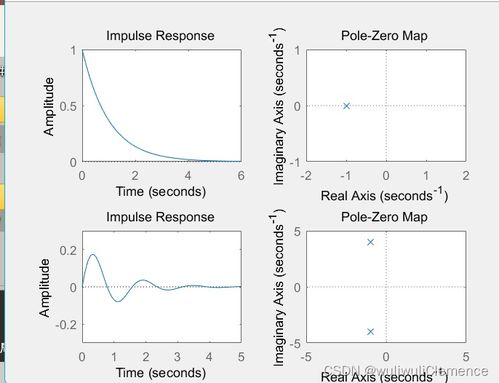
roots：用于求解多项式的根，即极点。函数调用格式为：roots(a)，其中a是多项式的系数向量。

poly：用于创建多项式，函数调用格式为：poly(a)，其中a是多项式的系数向量。

tf：用于创建传递函数，函数调用格式为：tf(num, den)，其中num是分子多项式的系数向量，den是分母多项式的系数向量。

poles：用于直接求解系统的极点，函数调用格式为：poles(sys)，其中sys是系统传递函数。

MATLAB求解极点的实例

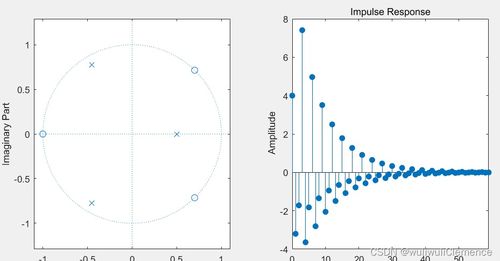
以下是一个使用MATLAB求解系统极点的实例：

```matlab

% 定义系统传递函数

num = [1 2 3]; % 分子多项式系数向量

den = [1 4 6 5]; % 分母多项式系数向量

sys = tf(num, den);

% 求解系统极点

poles = poles(sys);

% 显示系统极点

disp('系统极点：');

disp(poles);

在上面的代码中，我们首先定义了一个系统传递函数，然后使用`poles`函数求解系统的极点，并将结果显示在控制台。

MATLAB绘制系统极点图

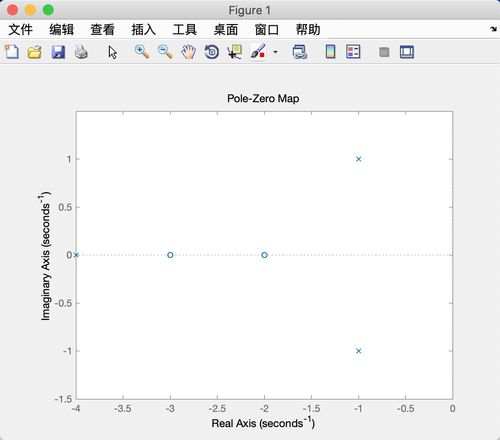
在MATLAB中，可以使用`pzmap`函数绘制系统的极点图。以下是一个绘制系统极点图的实例：

```matlab

% 绘制系统极点图

pzmap(sys);

在上面的代码中，我们使用`pzmap`函数绘制了系统传递函数的极点图，其中极点用'x'表示，零点用'o'表示。

MATLAB求解极点的实际应用

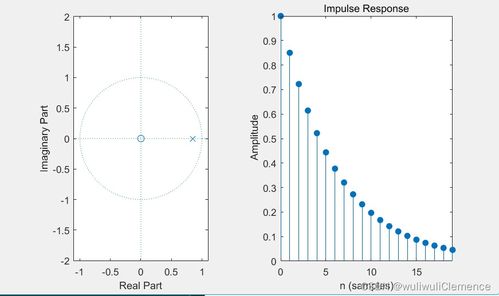
系统稳定性分析：通过求解系统极点，可以判断系统是否稳定，以及稳定性的程度。

系统响应速度分析：通过分析系统极点的实部和虚部，可以判断系统的响应速度。

系统超调量分析：通过分析系统极点的实部和虚部，可以判断系统的超调量。

本文介绍了如何在MATLAB中求解系统的极点，包括基本概念、常用函数以及实际应用案例。通过使用MATLAB提供的函数和工具，可以方便地求解系统的极点，并分析系统的动态特性。在实际应用中，合理运用MATLAB求解极点，有助于提高控制系统的性能和稳定性。