matlab系统的时域分析,系统时域分析的基本概念

随着计算机技术的飞速发展，MATLAB作为一种高性能的数学计算软件，在各个领域得到了广泛的应用。在信号与系统领域，MATLAB强大的数值计算和图形显示功能，使得系统的时域分析变得更加直观和高效。本文将详细介绍MATLAB在系统时域分析中的应用，包括基本概念、常用函数以及实际案例分析。

系统时域分析的基本概念

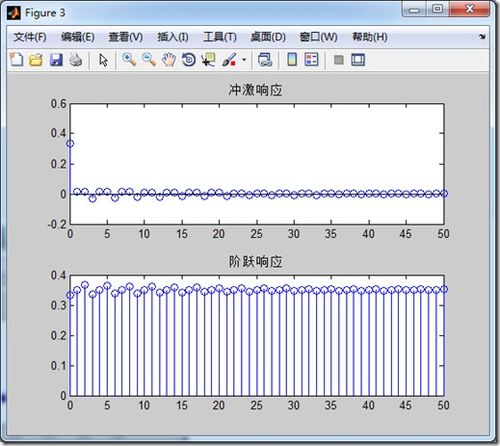
系统时域分析是研究系统对输入信号的响应特性的一种方法。它主要关注系统在时间域内的动态行为，包括系统的稳定性、响应速度、超调量等性能指标。在MATLAB中，系统时域分析主要包括以下内容：

系统微分方程的求解

系统传递函数的求解

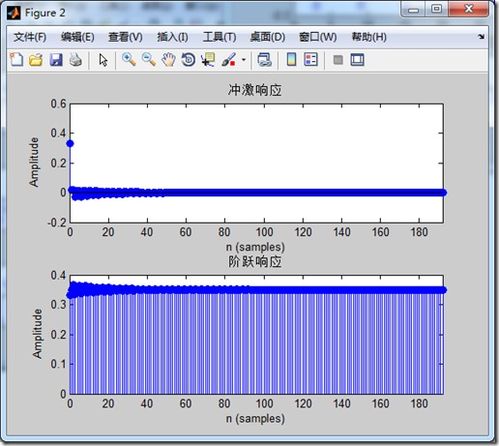
系统冲激响应和阶跃响应的求解

系统卷积运算的求解

MATLAB常用函数

ode45：用于求解常微分方程组，适用于连续时间系统。

tf：用于创建传递函数模型。

impulse：用于计算系统的冲激响应。

step：用于计算系统的阶跃响应。

conv：用于计算两个信号的卷积。

实际案例分析

以下将通过一个实际案例，展示如何使用MATLAB进行系统时域分析。

案例：二阶系统的时域分析

假设我们有一个二阶系统，其传递函数为：

$$H(s) = frac{K}{s^2 + 2zetaomega_ns + omega_n^2}$$

其中，K为系统增益，$zeta$为阻尼比，$omega_n$为自然频率。

我们的目标是分析该系统在不同阻尼比下的阶跃响应和冲激响应。

1. 创建传递函数模型

num = [K]; % 系统增益

den = [1 2zetawn wn^2]; % 系统传递函数的分子和分母

sys = tf(num, den); % 创建传递函数模型

2. 计算阶跃响应

figure;

step(sys); % 绘制阶跃响应曲线

xlabel('时间 (s)');

ylabel('输出');

title('二阶系统的阶跃响应');

3. 计算冲激响应

figure;

impulse(sys); % 绘制冲激响应曲线

xlabel('时间 (s)');

ylabel('输出');

title('二阶系统的冲激响应');

通过以上步骤，我们可以得到二阶系统在不同阻尼比下的阶跃响应和冲激响应曲线，从而分析系统的动态特性。

本文介绍了MATLAB在系统时域分析中的应用，包括基本概念、常用函数以及实际案例分析。通过MATLAB，我们可以方便地求解系统微分方程、传递函数、冲激响应和阶跃响应，从而分析系统的动态特性。在实际应用中，MATLAB为信号与系统领域的研究提供了强大的工具支持。