matlab 系统冲激响应,冲激响应的概念

在信号与系统领域，系统冲激响应是描述系统对单位冲激信号响应的重要指标。MATLAB作为一种强大的数学计算软件，在信号与系统分析中有着广泛的应用。本文将介绍如何使用MATLAB求解系统的冲激响应，并探讨其在实际工程中的应用。

冲激响应的概念

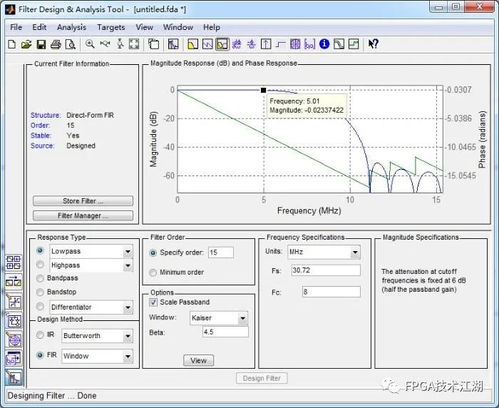
冲激响应是指系统对单位冲激信号的响应。单位冲激信号是一种理想化的信号，其数学表达式为δ(t)，即在t=0时取值为无穷大，其余时间取值为0。在连续时间系统中，冲激响应可以通过求解系统的微分方程得到；在离散时间系统中，则通过求解差分方程得到。

使用MATLAB求解连续时间系统冲激响应

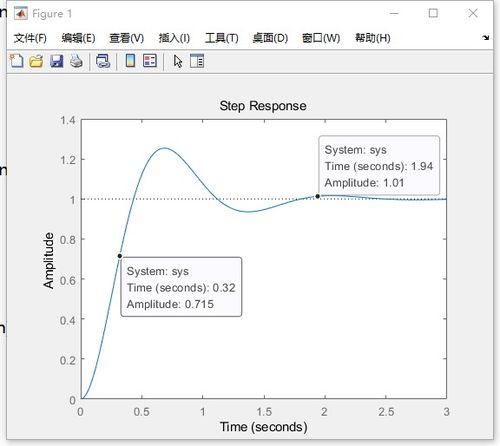
在MATLAB中，可以使用控制系统工具箱提供的函数impulse求解连续时间系统的冲激响应。以下是一个使用impulse函数求解冲激响应的示例：

```matlab

% 定义系统传递函数

num = [1 0];

den = [1 2 3];

sys = tf(num, den);

% 求解冲激响应

[y, t] = impulse(sys);

% 绘制冲激响应曲线

plot(t, y);

xlabel('时间 (s)');

ylabel('冲激响应');

title('连续时间系统冲激响应');

grid on;

在上面的代码中，我们首先定义了系统的传递函数，然后使用impulse函数求解冲激响应。最后，我们使用plot函数绘制冲激响应曲线。

使用MATLAB求解离散时间系统冲激响应

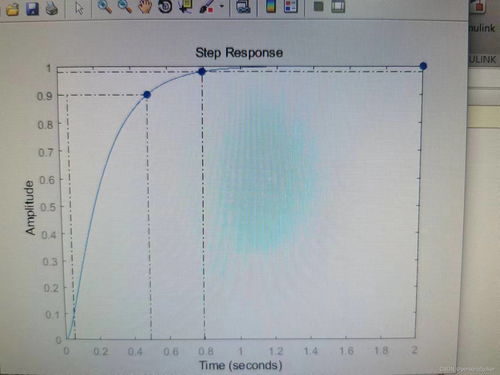
在MATLAB中，可以使用控制系统工具箱提供的函数impz求解离散时间系统的冲激响应。以下是一个使用impz函数求解冲激响应的示例：

```matlab

% 定义系统差分方程系数

b = [1 -2 3];

a = [1 -4 2];

% 求解冲激响应

[y, n] = impz(b, a);

% 绘制冲激响应曲线

plot(n, y);

xlabel('时间 (n)');

ylabel('冲激响应');

title('离散时间系统冲激响应');

grid on;

在上面的代码中，我们首先定义了系统的差分方程系数，然后使用impz函数求解冲激响应。最后，我们使用plot函数绘制冲激响应曲线。

冲激响应的应用

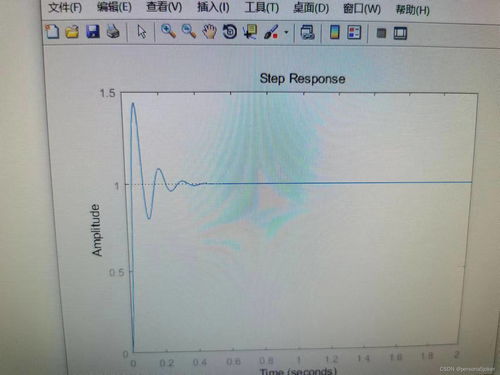
系统稳定性分析：通过观察冲激响应的衰减情况，可以判断系统是否稳定。

系统性能分析：通过分析冲激响应的形状，可以了解系统的瞬态响应和稳态响应特性。

系统辨识：通过比较实际系统的冲激响应与理论模型的冲激响应，可以识别系统的参数。

结论

本文介绍了如何使用MATLAB求解系统的冲激响应，并探讨了其在实际工程中的应用。通过MATLAB强大的数学计算功能，我们可以方便地分析系统的动态特性，为工程实践提供理论依据。