matlab求系统的响应曲线,MATLAB求系统响应曲线的详细指南

MATLAB求系统响应曲线的详细指南

在控制系统设计中，了解系统的响应曲线对于评估系统的性能至关重要。MATLAB作为一种强大的数学计算和仿真软件，提供了丰富的工具来绘制和分析系统的响应曲线。本文将详细介绍如何在MATLAB中求取系统的响应曲线，并探讨相关的应用。

一、系统响应曲线概述

系统响应曲线是指系统在受到外部输入信号作用时，输出信号的时域变化情况。常见的系统响应曲线包括单位阶跃响应、单位脉冲响应和单位斜坡响应等。通过分析这些响应曲线，可以评估系统的稳定性、快速性和准确性。

二、MATLAB绘制系统响应曲线

在MATLAB中，可以使用以下几种方法绘制系统的响应曲线：

1. 使用`step`函数

`step`函数是MATLAB中用于绘制系统单位阶跃响应的常用函数。其基本语法如下：

step(sys)

其中，`sys`是系统的传递函数模型。例如，绘制一个典型二阶系统的单位阶跃响应曲线，可以使用以下代码：

num = [1 2]; % 分子系数

den = [1 2 1]; % 分母系数

sys = tf(num, den); % 构造传递函数模型

step(sys); % 绘制单位阶跃响应曲线

2. 使用`impulse`函数

`impulse`函数用于绘制系统的单位脉冲响应曲线。其基本语法如下：

impulse(sys)

例如，绘制上述二阶系统的单位脉冲响应曲线，可以使用以下代码：

impulse(sys); % 绘制单位脉冲响应曲线

3. 使用`lsim`函数

`lsim`函数可以用于绘制系统在任意输入信号作用下的响应曲线。其基本语法如下：

lsim(sys, u, t)

其中，`u`是输入信号向量，`t`是时间向量。例如，绘制系统在单位斜坡信号作用下的响应曲线，可以使用以下代码：

u = [0:0.01:10]; % 单位斜坡信号

t = 0:0.01:10; % 时间向量

lsim(sys, u, t); % 绘制单位斜坡响应曲线

三、系统响应曲线分析

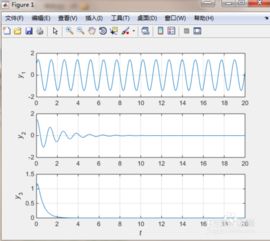
在MATLAB中绘制出系统响应曲线后，可以对以下方面进行分析：

1. 稳定性分析

通过观察系统响应曲线，可以初步判断系统的稳定性。如果系统在有限时间内趋于稳定，则认为系统是稳定的；如果系统出现发散或振荡，则认为系统是不稳定的。

2. 速度和精度分析

通过分析系统响应曲线的上升时间、下降时间、超调量和调节时间等参数，可以评估系统的速度和精度。这些参数对于控制系统设计具有重要意义。

3. 特征参数分析

通过分析系统响应曲线，可以提取系统的特征参数，如阻尼比、自然频率等。这些参数对于控制系统设计、分析和优化具有重要意义。

本文详细介绍了如何在MATLAB中求取系统的响应曲线，并探讨了相关的应用。通过使用MATLAB提供的函数和工具，可以方便地绘制和分析系统的响应曲线，为控制系统设计提供有力支持。