LTI系统分析,LTI系统的定义与特性

线性时不变（Linear Time-Invariant，简称LTI）系统是工程和科学领域中广泛存在的一类系统。这类系统具有线性、时不变的特点，使得其在信号处理、控制系统、通信系统等领域有着重要的应用。本文将对LTI系统的基本概念、特性以及分析方法进行探讨。

LTI系统的定义与特性

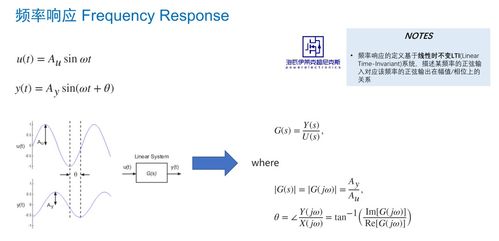
LTI系统是指输入信号与输出信号之间满足线性叠加原理和时不变性的系统。具体来说，对于任意两个输入信号x1(t)和x2(t)，以及任意两个常数a和b，系统输出y(t)满足以下条件：

线性叠加性：y(t) = ay1(t) + by2(t)，其中y1(t)和y2(t)分别是x1(t)和x2(t)的输出。

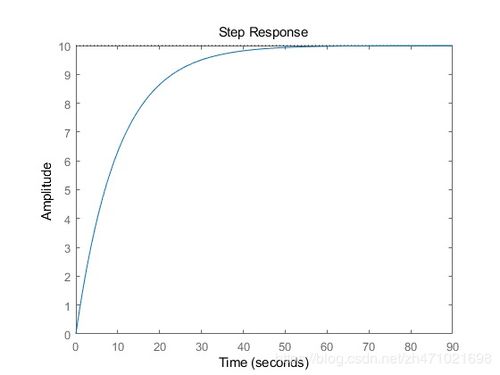
时不变性：如果输入信号x(t)经过时间t0平移后变为x(t-t0)，则输出信号y(t)也相应地平移t0，即y(t) = y(t-t0)。

LTI系统的这些特性使得其在分析和设计过程中具有很大的便利性。

LTI系统的数学模型

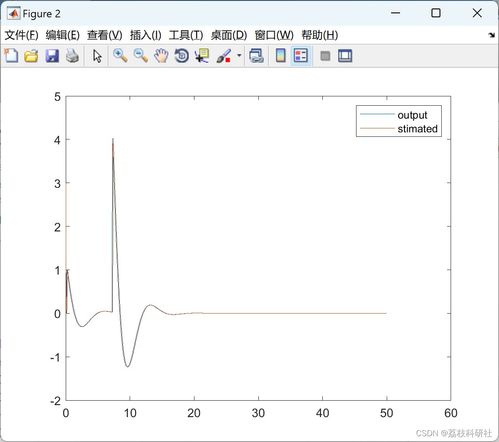
LTI系统的数学模型通常采用传递函数或状态空间表示。传递函数H(s)表示系统在复频域内的输入输出关系，而状态空间表示则描述了系统在时域内的动态特性。

传递函数：H(s) = Y(s)/X(s)，其中Y(s)和X(s)分别是输出信号和输入信号的拉普拉斯变换。

状态空间表示：x'(t) = Ax(t) + Bu(t)，y(t) = Cx(t) + Du(t)，其中x(t)是状态变量，u(t)是输入信号，y(t)是输出信号，A、B、C、D是系统矩阵。

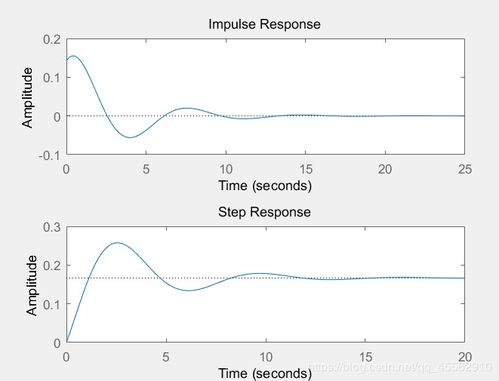
通过传递函数或状态空间表示，可以方便地分析LTI系统的稳定性、频率响应、传递函数等特性。

LTI系统的稳定性分析

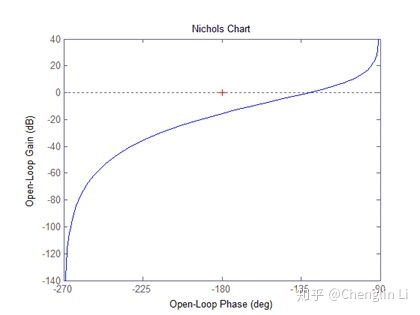
LTI系统的稳定性是系统设计的重要指标之一。根据系统矩阵A的特征值，可以判断系统的稳定性。具体来说，有以下几种稳定性判据：

Hurwitz判据：如果系统矩阵A的所有特征值都具有负实部，则系统是稳定的。

Nyquist判据：如果系统传递函数H(s)在右半平面没有极点，且满足Nyquist准则，则系统是稳定的。

Bode判据：如果系统传递函数H(s)在右半平面没有极点，且满足Bode准则，则系统是稳定的。

稳定性分析对于确保系统在实际应用中的可靠性和安全性具有重要意义。

LTI系统的频率响应分析

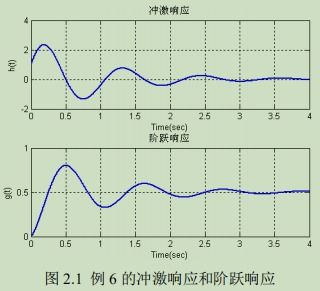
LTI系统的频率响应描述了系统对不同频率信号的响应特性。通过分析频率响应，可以了解系统的幅频特性、相频特性以及群延迟等参数。

幅频特性：描述了系统输出信号的幅度与输入信号频率之间的关系。

相频特性：描述了系统输出信号的相位与输入信号频率之间的关系。

群延迟：描述了系统输出信号中不同频率成分的延迟时间。

频率响应分析对于优化系统性能、设计滤波器等具有重要意义。

LTI系统的传递函数设计

LTI系统的传递函数设计是系统设计的重要环节。通过设计合适的传递函数，可以实现以下目标：

满足系统性能指标：如稳态误差、过渡过程时间、上升时间等。

提高系统稳定性：如增加系统的阻尼比、降低系统的自然频率等。

优化系统频率响应：如设计带通滤波器、低通滤波器等。

传递函数设计方法包括经典控制理论、现代控制理论以及计算机辅助设计等。

结论

LTI系统在工程和科学领域中具有广泛的应用。通过对LTI系统的基本概念、特性以及分析方法进行探讨，有助于我们更好地理解和应用这类系统。在实际应用中，合理分析和设计LTI系统，可以确保系统在实际应用中的可靠性和安全性。