l系统 分形,L系统的基本原理

L系统分形是一种基于数学模型的图形生成方法，它通过迭代和递归的方式生成具有自相似性的复杂图形。L系统分形在计算机图形学、植物形态学、艺术创作等领域有着广泛的应用。本文将介绍L系统的基本原理、分形的生成过程以及L系统分形的应用。

L系统的基本原理

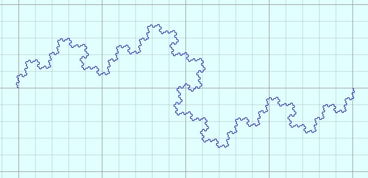
L系统（Lindenmayer System）是由匈牙利生物学家Aristid Lindenmayer于1968年提出的一种数学模型。它主要用于模拟植物的生长过程，但也可以用于生成各种复杂的图形。L系统由以下几个部分组成：

符号变量集合（V）：定义了L系统中使用的符号。

常量符号集合（S）：定义了L系统中使用的常量符号。

初始状态串（axiom）：L系统的起始字符串。

生成规则（P）：定义了符号之间的替换规则。

L系统分形的生成过程

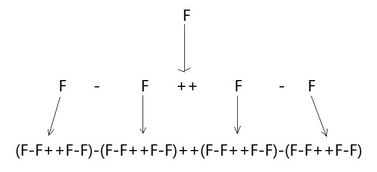
L系统分形的生成过程主要包括以下几个步骤：

初始化：根据L系统的定义，设置符号变量集合、常量符号集合、初始状态串和生成规则。

迭代：根据生成规则，对初始状态串进行迭代替换，生成新的字符串。

图形化：将迭代后的字符串转换为图形，生成分形图形。

递归：根据需要，对生成的图形进行递归处理，进一步增加图形的复杂度。

示例：L系统分形的生成

以下是一个简单的L系统分形生成示例：

符号变量集合（V）：A

常量符号集合（S）：无

初始状态串（axiom）：A

生成规则（P）：A → AB

根据上述规则，我们可以得到以下迭代过程：

初始状态串：A

第一次迭代：AB

第二次迭代：ABA

第三次迭代：ABABA

将迭代后的字符串转换为图形，我们可以得到一个简单的L系统分形图形。

L系统分形的应用

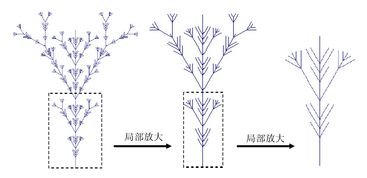
计算机图形学：L系统分形可以用于生成各种复杂的图形，如植物、动物、自然景观等。

植物形态学：L系统分形可以用于模拟植物的生长过程，研究植物形态的演化规律。

艺术创作：L系统分形可以用于创作独特的艺术作品，如绘画、雕塑等。

计算机辅助设计：L系统分形可以用于生成复杂的几何形状，辅助设计师进行设计。

L系统分形是一种基于数学模型的图形生成方法，具有自相似性、递归性等特点。通过L系统分形，我们可以生成各种复杂的图形，并在计算机图形学、植物形态学、艺术创作等领域得到广泛应用。随着计算机技术的不断发展，L系统分形的应用前景将更加广阔。