matlab 系统稳定,理论与实践

MATLAB系统稳定性分析：理论与实践

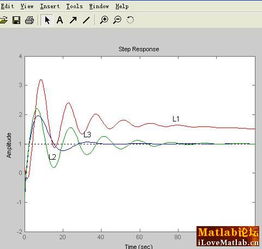
在工程和科学领域，系统稳定性分析是一个至关重要的环节。MATLAB作为一种强大的计算软件，提供了丰富的工具和函数来帮助用户进行系统稳定性分析。本文将探讨MATLAB在系统稳定性分析中的应用，包括理论背景、常用方法以及实际案例分析。

一、系统稳定性理论背景

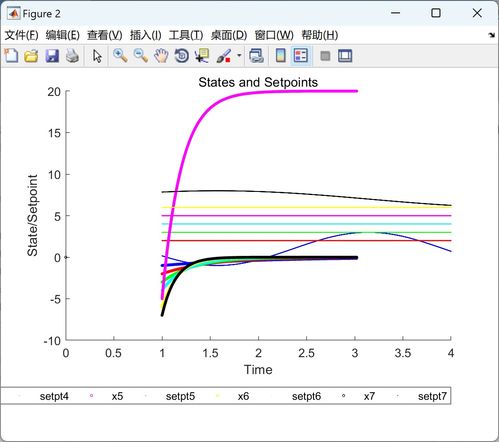
系统稳定性是指系统在受到扰动后，能否回到初始状态或稳定在某个平衡点。根据系统动态特性的不同，稳定性可以分为以下几种类型：

渐近稳定性：系统在受到扰动后，随着时间的推移，状态变量会逐渐趋向于平衡点。

稳定平衡点：系统在受到扰动后，能够稳定在平衡点附近。

不稳定平衡点：系统在受到扰动后，状态变量会远离平衡点。

二、MATLAB系统稳定性分析方法

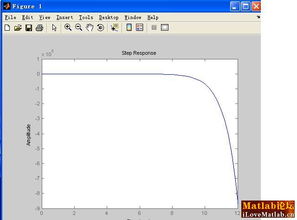
根轨迹分析：通过绘制系统传递函数的根轨迹，可以直观地观察系统稳定性随参数变化的情况。

频率响应分析：通过绘制系统传递函数的频率响应曲线，可以分析系统在不同频率下的稳定性。

Nyquist图分析：根据Nyquist准则，通过绘制系统传递函数的Nyquist图，可以判断系统稳定性。

Bode图分析：通过绘制系统传递函数的Bode图，可以分析系统稳定性随频率变化的情况。

三、MATLAB系统稳定性案例分析

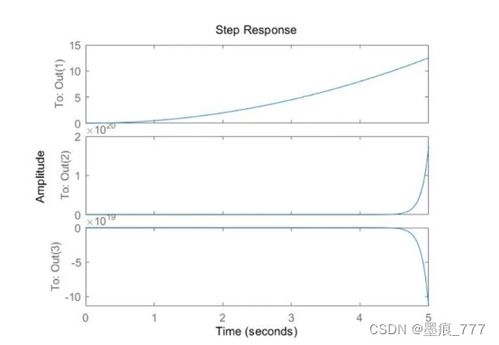
以下是一个基于MATLAB的系统稳定性分析案例，我们将使用根轨迹分析来研究一个简单的二阶系统。

案例：二阶系统稳定性分析

假设我们有一个二阶系统，其传递函数为：

[ G(s) = frac{K}{(s+a)(s+b)} ]

其中，( K ) 是增益，( a ) 和 ( b ) 是系统参数。

为了分析系统的稳定性，我们可以使用MATLAB的`rlocus`函数来绘制根轨迹。以下是MATLAB代码示例：

num = [1]; % 分子系数

den = [1, a, b]; % 分母系数

rlocus(num, den);

通过观察根轨迹，我们可以发现，当增益 ( K ) 增大时，系统根轨迹会向右移动，最终进入右半平面，导致系统不稳定。因此，我们需要调整系统参数或增益，以确保系统稳定性。

MATLAB在系统稳定性分析中具有广泛的应用。通过使用MATLAB提供的工具和函数，我们可以方便地进行系统稳定性分析，从而为工程和科学研究提供有力支持。在实际应用中，我们需要根据具体问题选择合适的方法，并结合理论知识进行分析，以确保系统稳定性和可靠性。